判断点在多边形内部还是外部

对任意给的一个多边形和一个已知点，如何判断该点在多边形的内部，外部还是就在多边形上？

如果给定的多边形是凸多边形

法一：如果点在四边形内，那么所有经过这个点的直线都会和边相交，并且一定是在两个交点之间。反之如果在四边形外，那么就有三种可能，一种是没交点，一种是一个交点，最后一种是两个交点。但因为是凸四边形所以必然不在中间。所以可以任取一条过点直线，判断该点是否在交点之间，就可以得出是否是在四边形内了。

法二：如果点在这个凸四边形内，那么按照逆时针方向走的话，该点一定会在每一条边的左边。

法一详解：

假设四边形为ABCD,给定点M(X3,Y3),过C的任意直线为a（x-X3)+b（y-Y3)=0。
任取一条过点直线l：x = X3,分别求出l与AB,BC, CD, DA的交点，并记录下来。
- 如果交点数<2,则在四边形外边
- 如果交点数=2，设为E、F：
  1）如果ME<EF&&MF<EF，则在四边形内部
  2）否则，在四边形外部。

法二详解：

按逆时针方向遍历这个凸四边形的每一条边的两个顶点A(X1,Y1)和B(X2,Y2)，构成矢量 AB = (X2-X1, Y2-Y1).
采用矢量叉积的方法判断一个点是否在一个矢量左边。
- 假设给定点C(X3,Y3)，AC = (X3-X1, Y3-Y1).
- AB和AC的叉积为（2*2的行列式）：
```
|X2-X1 Y2-Y1|
|X3-X1 Y3-Y1|
```
  值为：ABAC =（X2-X1)(Y3-X1) - (Y2-Y1)*(X3-X1)
- 利用右手法则进行判断：
  
  如果ABAC > 0,则点C在矢量AB的左边；
  如果ABAC < 0,则点C在矢量AB的右边。
按照逆时针方向，对凸四边形的每一条边都如此判断，如果每次都判断出C在左边，那么就说明这个点在凸多边形内部了。

如果给定的多边形是凹多边形

先在凹多边形上添加一些边，使得凹多边形变成凸多边形，然后再按照凸多边形的方法去判断。示例图如下：

对于凹多边形ABCDEFGH，补边BE和FH(图中虚线所示)，则可以构成三个凸多边形：凸多边形ABEFH，凸多边形BCDE和凸多边形FGH，然后判断给定点与这三个凸多边形的关系。

如果给定点在凸多边形ABEFH内部，而在凸多边形BCDE和凸多边形FGH的外部，那么就可以说明给定点在多边形ABCDEFGH的内部了。

下面就分别说明如何判断一个三角形是逆时针还是顺时针，如何判断一个多边形的凹凸性，如何补边，以及如何通过补边构造凸多边形。只要构造出所有的凸多边形，就可以按照上述第二种情况判断了。

经过上面的所有分析，就可以轻松判断任意一个点是否在一个给定多边形的内部了。

判断一个三角形的顺时针还是逆时针

可以利用矢量叉积来判断一个给定的三角形是逆时针还是顺时针。

假设给定三角形的三个顶点A(x1,y1),B(x2,y2),C(x3,y3),构造三角形两边的矢量分别是：

AB=(x2-x1,y2-y1), AC=(x3-x1,y3-y1)

则AB和AC的叉积为：

|x2-x1, y2-y1|
|x3-x1, y3-y1|

值为：r = (x2-x1)(y3-y1) - (y2-y1)(x3-x1)

然后利用右手法则进行判断：

如果r>0,则三角形ABC是逆时针的
如果r<0,则三角形ABC是顺时针的
这样就可以判断一个给定三角形是顺时针还是逆时针了。

(如果这里你发现计算出r=0，那么说明ABC三点共线，即给定点在多边形的边上，可以直接返回)

判断一个多边形的凹凸性。

利用上述判断三角形是顺时针还是逆时针的方法来辅助判断一个多边形的凹凸性。

对于一个给定的多边形，按照逆时针方向遍历该多边形的所有顶点，并放入一个首尾相连的循环链表中。然后从这个循环链表中每次取出相邻三个顶点，判断这个三个顶点构成的三角形是顺时针三角形还是逆时针三角形，如果是逆时针，则说明该三角形三个顶点中位于中间的顶点是凸点；如果是顺时针，则说明位于中间的顶点是凹点。

例如：假设取出的三个顶点是A、B、C，如果三角形ABC是逆时针三角形，则说明顶点B(即位于中间的顶点)是凸点，否则是凹点。然后可以取出D点，通过三角形BCD判断C点的凹凸性，同理D点，E点…最后也可以判断出A点的凹凸性。(通过由最后一个顶点，A点,B点按顺序构成的三角形来判断A点的凹凸性)。如果该多边形所有的顶点经过判断都是凸点，则说明该多边形是凸多边形，否则就是凹多边形。

对于上述示例用图，多边形ABCDEFGH中，点A，B，E，F，H是凸点，点C，D，G是凹点。由于并不是所有的顶点都是凸点，所以多边形ABCDEFGH是凹多边形。

补边

利用上述对给定多边形的每一个顶点的凹凸性的判断来进行补边操作。

补边算法：

从存储多边形顶点的循环链表中，找到一个凸点(一定存在这个凸点，即不可能所有顶点都是凹点)
从这个顶点开始往后遍历顶点，当遇到的第一个凹点时标记紧邻这个凹点的前一个凸点，因为这个凸点就是所需要补的边的一个顶点，然后继续往后遍历，如果还是凹点，跳过继续遍历，直至找到第一个凸点，那么这个凸点就是所需要补的边的另一个顶点。这样就找出了所需要补的边的两个顶点，就可以确定需要补的一条边了。
从找到的凸点开始，重复上述第2步操作。直至回到最开始找到的凸点，则算法结束。这样就可以找到所有需要补的边了。
可以发现，每一条补边，起点和终点都是凸点，中间经过的顶点都是凹点。

上述示例用图中，对于补边BE，顶点B和E都是凸点，而它们中间的顶点C和D则都是凹点。对于补边FH，顶点F和H都是凸点，而它们中间的顶点G则是凹点。

构造凸多边形

利用上述补边来构造凸多边形。

算法如下：

对于找到每一条补边，起点和终点都知道，就可以从多边形顶点的循环链表中取出这两个顶点中间的所有的顶点，而这些顶点加上起点和终点就构成了一个外在凸多边形(即不属于原始多边形的多边形)。
示例中，外在凸多边形有凸多边形BCDE和凸多边形FGH。
在原始多边形顶点的循环链表中把所有的凹点都去除，只留下凸点。那么这些凸点即构成了原始多边形经补边之后构造的大凸多边形了。
示例中，去除所有凹点C，D，G，则剩下的顶点A,B,E,F,G构成了补边之后的大凸多边形ABEFH

附注：

矢量叉积

设矢量 P = (x1, y1), Q = (x2, y2)，则 P Q = x1 y2 - x2 y1; 其结果是一个由 (0, 0), P, Q, P + Q 所组成的平行四边形的带符号的面积，P Q = -(Q P), P (- Q) = -(P * Q)

叉积的一个非常重要的性质是可以通过它的符号来判断两矢量相互之间的顺逆时针关系：

若 PQ > 0，则 P 在 Q 的顺时针方向；
若 PQ < 0, 则 P 在 Q 的逆时针方向；
若 P*Q = 0，则 P 与 Q 共线，但不确定 P, Q 的方向是否相同。

折线段的拐向判断

如图，假设有折线段 p0p1p2 ，要确定 p1p2 相对于 p0p1 是向左拐还是向右拐，可以通过计算(p2 - p0)*(p1 - p0) 的符号来确定折线的拐向（点 p2 - p0 实际上就是向量 p2，但这里要注意线段和矢量的区别）。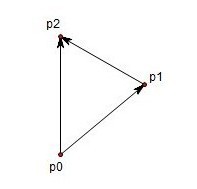

判断点是否在线段上
设点 Q = (x, y), P1 = (x1, y1), P2 = (x2, y2)，若 (Q - P1)*(P2 - P1) = 0 且 min(x1, x2) <= x <= max(x1, x2) && min(y1, y2) <= y <= max(y1, y2)，则点 Q 在线段 P1P2 上

判断两线段是否相交

1）快速排斥试验

设以线段 P1P2 为对角线的矩形为 R，设以线段 Q1Q2 为对角线的矩形为 T，若 R、T 不相交，则两线段不可能相交

假设 P1 = (x1, y1), P2 = (x2, y2), Q1 = (x3, y3), Q2 = (x4, y4)，设矩形 R 的 x 坐标的最小边界为 minRX = min(x1, x2)，以此类推，将矩形表示为 R = (minRX, minRY, maxRX, maxRY) 的形式，若两矩形相交，则相交的部分构成了一个新的矩形 F，如图所示，我们可以知道 F 的 minFX = max(minRX, minTX), minFY = max(minRY, minTY), maxFX = min(maxRX, maxTX), maxFY = min(maxRY, maxTX)，得到 F 的各个值之后，只要判断矩形 F 是否成立就知道 R 和 T 到底有没有相交了，若 minFX > maxFX 或 minFY > maxFy 则 F 无法构成，RT不相交，否则 RT相交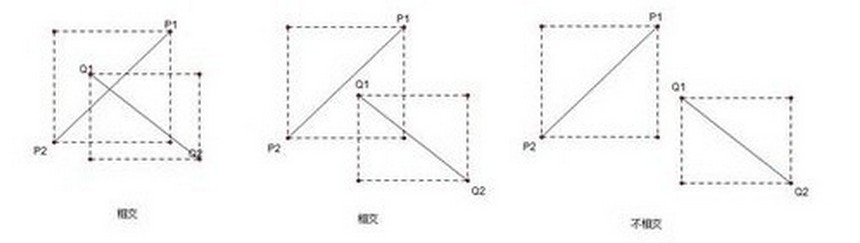

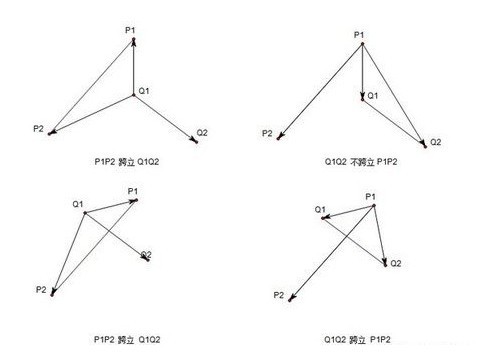
2）跨立试验

若 P1P2 跨立 Q1Q2，则 P1,P2 分别在 Q1Q2 所在直线的两端，则有 (P1 - Q1)(Q2 - Q1) (Q2 - Q1)(P2 - Q1) > 0，当 (P1 - Q1)(Q2 - Q1) = 0 时，说明 (P1 - Q1) 与 (Q2 - Q1) 共线，但由于已经经过快速排斥试验，所以 Q1 必为 P1P2 与 Q1Q2 的交点，依然满足线段相交的条件，则跨立试验可改为：

当 (P1 - Q1)(Q2 - Q1) (Q2 - Q1)*(P2 - Q1) >= 0，则 P1P2 跨立 Q1Q2，当 Q1Q2 也跨立 P1P2 的时候，则 P1P2 相交

（注意式子中被隔开的 代表两个叉积的值的相乘，而另外的两个 则代表计算矢量叉积）